In this section, we will show an example of nested classes for representing the concept of a context free grammar. We are thus in the domain of grammars from programming languages.
In qBeta – a new object-oriented language for programming and modeling a context free grammar to define the syntax of qBeta which we use in this book.
A context free grammar consists of:
- A set of Nonterminal symbols.
- A set of Terminal symbols.
- A set of Rules.
- A distinguished Nonterminal called the Start symbol.
The sets of nonterminal and terminal symbols are disjoint, i.e. no symbol can be both a nonterminal and a terminal. A symbol is either a nonterminal or a terminal symbol.
We define a class Grammar to represent the idea of a context-free grammar. Instances of this class represent grammars of specific languages like Java and Simula.
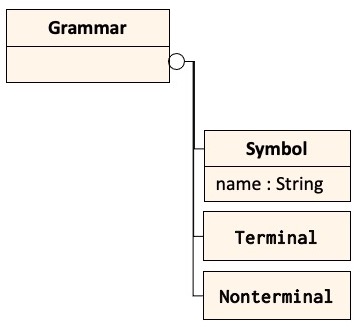
Class Grammar defines the symbols (nonterminals and terminals) of a given grammar. Different concrete grammars have different symbols. Java symbols differ from Simula symbols. We reflect this property in the definition of the Grammar class. The same applies to the rules of a given grammar. Different grammars have different rules and this is also be reflected in the definition of class Grammar. We use nested classes for this purpose as shown in the first sketch of class Grammar:
class Grammar:
nonterminals: obj Set(Nonterminal)
terminals: obj Set(Terminal)
rules: obj OrderedList(Rule)
start: ref Nonterminal
class Symbol(name: var String):
...
class Nonterminal: Symbol
...
class Terminal: Symbol
...
class Rule:
...The nonterminals are represented by a set of Nonterminal symbols and the terminals are represented by a set of Terminal symbols. The rules are represented by an OrderedList of Rule-objects. The Start symbol is represented by a reference, start to a Nonterminal.
The reason we use OrderedList to represent the rules and not Set as for Nonterminals and Terminals, is that we want to control the order of the rules when e.g. printing as shown below,
The fact that terminals and nonterminals are special symbols is represented by the classes Terminal and Nonterminal are subclasses of the class Symbol.
All these classes are local classes of Grammar, as they are parts of the definition Grammar. The Symbol class has a parameter, representing name of the Symbol.

The figures below show two different diagrams for illustrating nested classes. In the first diagram, the circle with a plus-sign (‘+‘) shows that class Grammar has local classes Symbol, Terminal and NonTerminal. In the second diagram, Symbol, Terminal and Nonterminal are shown inside the Grammar class – in addition, the class/subclass relations between Symbol, Terminal and NonTerminal are shown, which is not the case in the first diagram. We use the two types of diagrams depending on what is to be illustrated.

We may declare an object representing a (tiny part) of a Java grammar as follows:
Java: obj Grammar
jClass: obj Terminal("class")
jStatic: obj Terminal("static")
... The object Java is a sub of Grammar and it contains the declaration of two terminal symbols representing the Java symbols class and static.
We may in a similar way declare an object representing grammar for SIMULA:
Simula: obj Grammar
sClass: obj Terminal("class")
sBegin: obj Terminal("begin")The symbols jClass and jStatic represent the Java symbols class and static and sClass and sBegin represent the Simula symbols class and begin. Note, even if jClass and sClass have the same name they represent the class-symbol of different grammars.
The next diagrams are similar to the diagrams above showing the nesting of Symbol, Terminal and NonTerminal in class Grammar. The difference is that the diagrams below show the nesting within instances of class Grammar – the Java Grammar-object and the Simula Grammar-object. As before, the circle with a plus-sign (‘+‘) is used to illustrate nesting in the leftmost diagram. It shows that the Java Grammar-object and the Simula Grammar-object both have local classes Symbol, Terminal and NonTerminal.
In the second diagram, Symbol, Terminal and Nonterminal are shown inside the Java– and Simula-objects respectively – in addition, the class/subclass relations between is shown, which is not the case in the first diagram. As said above, we use the two types of diagrams depending on what is to be illustrated.
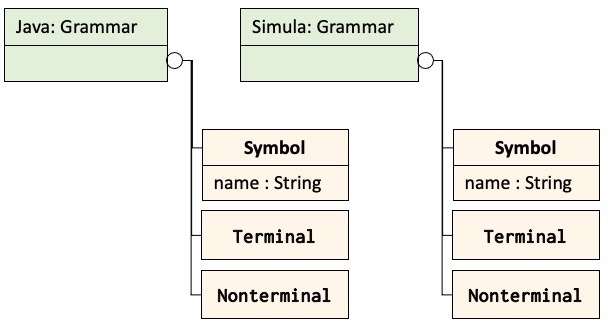

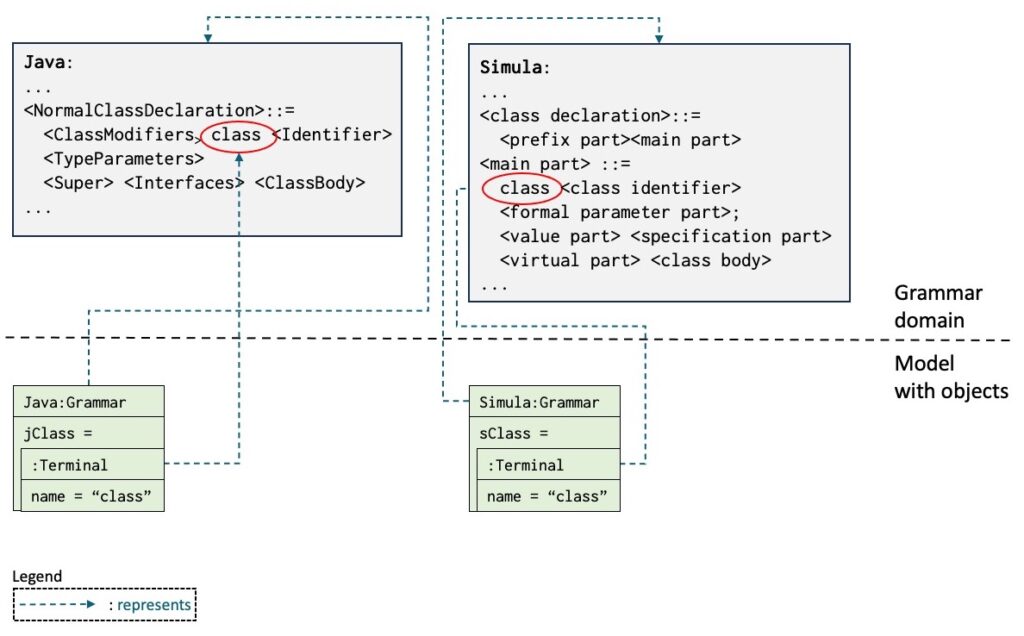
Java and Simula are both instances of the same class Grammar. The objects jClass, jStatic and sClass, sBegin are, however, not instances of the same class; jClass, and jStatic are instances of class Java.Terminal, whereas sClass, and sBegin are instances of class Simula.Terminal. The following figure illustrates this for jClass and sClass.
From a modeling point of view, this is what we want, since jClass, jStatic are Java symbols and sClass, sBegin are Simula symbols. The two classes of symbols are clearly different.
At this point we have not added the necessary content to the Java.nonterminals, Java.terminals, Java.rules and Java.start in order to represent a complete grammar for Java and similarly for Simula. These grammars are large and will thus take up a lot of space in this book. Instead, we show a complete example of a grammar for a subset of arithmetic expressions in section below.
In the next version of Grammar, we add a print method:
class Grammar:
nonterminals: obj Set(Nonterminal)
terminals: obj Set(Terminal)
rules: obj OrderedList(Rule)
start: ref Nonterminal
...
print:
console.print("Grammar:\n")
rules.scan
current.printThe print method prints the text "Grammar" and then it scans through the rules and invoke print on each rule in the grammar. And as mentioned above, we want to print the rules in the order we have added them to the OrderedList. See the expression grammar example below for details.
The difference between Java.Symbol and Simula.Symbol is the same as the difference between Java.Print and Simula.Print. The latter two expressions invoke different Print method objects, since they have different contexts. Figure X1 shows a diagram representing the objects Java and Simula.
Figure ~\ref{fig:symbdiagram} shows the objects Java, Simula, jClass, jStatic and sClass, sBegin. Note that jClass, jStatic and sClass, sBegin have different origins.
By declaring Symbol local to the Grammar class, we have the possibility of distinguishing between symbols of different grammars. Also, since the class Symbol is local to Grammar, a Symbol has no existence without a Grammar object. From a modeling point of view, this is what we want.
In the example above, the data-items jClass, jStatic and sClass, sBegin are constant references in the sense that they each of them refer to the same object during the whole of the program execution. It is, of course, also possible to declare variable references using ref. In the example below we declare data-items where the type is a remote name:
aJavaSymbol: ref Java.Symbol
aSimulaSymbol: ref Simula.SymbolThe reference aJavaSymbol may denote any instance of Java.Symbol and aSimulaSymbol may denote any instance of Simula.Symbol. It is important emphasise that these two data-items have different types. Class Symbol in Java is different from class Symbol in Simula.
Suppose that we want to declare a reference that can denote arbitrary symbols of any Grammar. This is done by declaring a variable reference qualified by Grammar.Symbol:
anySymbol: ref Grammar.SymbolNote the difference from the declaration of aJavaSymbol using Java.Symbol, where Java is a reference to a Grammar object. In the declaration of anySymbol, Grammar is a class name. anySymbol can refer to instances of either Java.Symbol or Simula.Symbol. In fact, the class Grammar.Symbol may be viewed as a generalization of the classes Java.Symbol and Simula.Symbol. The Grammar.Symbol class is then a representation of the general concept of a symbol of a context free grammar.
