In this section, we show examples of how to use coroutines to describe a certain class of algorithms often referred to as interlocked sequential execution stacks.
A generator is a coroutine capable of producing a sequence of values. A new value is produced for each invocation of the coroutine. The next value depends on the sequence of previously generated values. We show how to define generators for computing the mathematical functions factorial. The main purpose of the factorial example is to illustrate how coroutines work.
We assume the reader is familiar with the factorial function, but here is a short description: The factorial of a non-negative integer N, denoted by N!, is the product of all positive integers less than or equal to N. First we show how to define factorial as a simple method:
FactorialFunction(N: var integer) -> F: var integer:
F := N
loop: do
if (N > 1) :then
N := N - 1
F := F * N
restart(loop)As can be seen, FactorialFunction computes the product N * (N – 1) * (N – 2) * … * 2 * 1.
Next we show how to define a generator that produce the sequence of factorial, 1!, 2!, 3!, …, N!, …. When the coroutine is resumed, it returns the next value in the sequence when it suspends.
PlainFactorial: obj
getNext -> R: var integer:
PlainFactorial.call
R := F
F: var integer
N: var integer
F := 1
cycle
PlainFactorial.suspend
N := N + 1
F := F * NWhen PlainFactorial is generated it executes statements until the first execution of PlainFactorial.suspend. An invocation of ++++
Explanation, perhaps OSD showing the recursion. PlainFactorial.getNext will then return the factorial of 1 which is 1. Subsequent invocations will return the next factorial as shown below:
UsingPlainFactorial: obj
PlainFactorial: obj
-"-
V: var integer
V := PlainFactorial.getNext -- V = 1
V := PlainFactorial.getNext -- V = 2
V := PlainFactorial.getNext -- V = 6
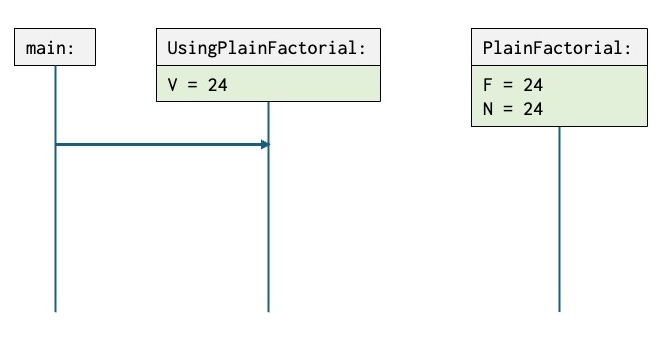
V := PlainFactorial.getNext -- V = 24The next figure shows a snapshot of the execution of UsingPlainFactorial where:
PlainFactorialhas been generated and suspended execution during the first iteration ofcycle.- The read arrow –> shows that
PlainFactorialis suspended just before the statementN := N + 1. - The point of execution in
UsingPlainFactorialis before the first statementV := PlainFactorial.nextas indicated by the read arrow ==>. - A read arrow of the form ==> shows the active point of execution.
- A read arrow of the form –> show the point of suspension of a coroutine.
The OSD in the right column illustrates that UsingPlainFactorial is currently executing and that PlainFactorial is suspended.
+++ Skal der forklares hvordan man kan se at den er suspended?
Den er ikke med i sekvensen som starter i main, og man ved jo at den er genereret, men det er vel ikke nok? OLM: måske nok!? Hvad kan den ellers være?
UsingPlainFactorial: obj
PlainFactorial: obj
-"-
F := 1
cycle
PlainFactorial.suspend
--> N := N + 1
F := F * N
V: var integer
==> V := PlainFactorial.getNext
V := PlainFactorial.getNext
V := PlainFactorial.getNext
V := PlainFactorial.getNext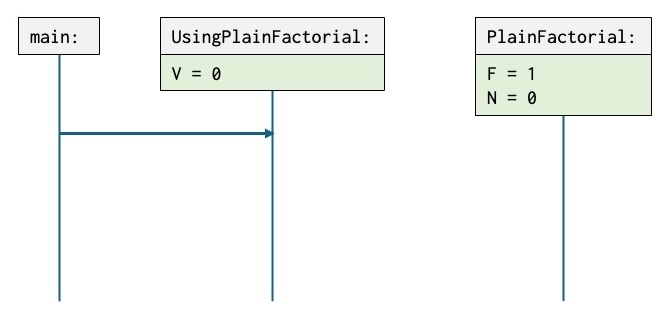
The OSD also shows the values of the variable V in UsingPlainFactorial, and the variables , F and N in PlainFactorial.
The next next scenario shows the situation:
PlainFactorial.getNexthas been executed byUsingPlainFactorial.getNexthas executedPlainFactorial.call.- The next statement to be executed is
N := N + 1.
UsingPlainFactorial: obj
PlainFactorial: obj
getNext -> R: var integer:
PlainFactorial.call
R := F
F: var integer
N: var integer
F := 1
cycle
PlainFactorial.suspend
==> N := N + 1
F := F * N
V: var integer
V := PlainFactorial.getNext
V := PlainFactorial.getNext
V := PlainFactorial.getNext
V := PlainFactorial.getNext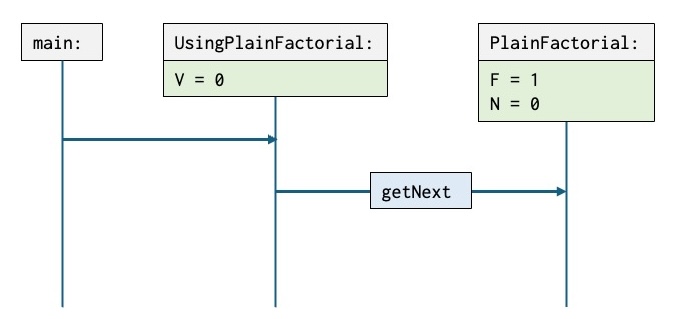
The next snapshot shows the situation after PlainFactorial has executed the two assignments statements, N := N + 1 and F := F * N, and executed a PlainFactorial.suspend during the second iteration of cycle:
PlainFactorialis suspended before the statementN := N + 1– as in the first figure above.- The active point of execution is in
UsingPlainFactorialbefore the second statementV := PlainFactorial.getNext. - The variables have been updated
V,FandNhave all new values.
UsingPlainFactorial: obj
PlainFactorial: obj
-"-
cycle
PlainFactorial.suspend
--> N := N + 1
F := F * N
V: var integer
V := PlainFactorial.getNext
==> V := PlainFactorial.getNext
V := PlainFactorial.getNext
V := PlainFactorial.getNext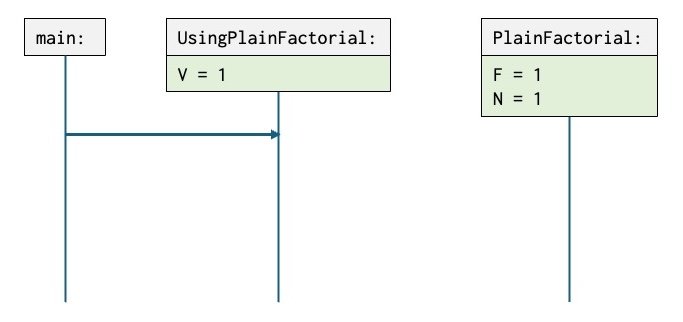
Execution of the second V := PlainFactorial.getNext resumes execution of PlainFactorial, which then generate the next factorial value. We don’t show a snapshot of this.
The next snapshot shows the situation after PlainFactorial has suspended:
PlainFactorialis as in previous snapshots suspended before the statementN := N + 1.- The current point of execution is in
UsingPlainFactorialbefore the third statementV := PlainFactorial.getNext. - The variables
V,FandNhave been updated.
UsingPlainFactorial: obj
PlainFactorial: obj
-"-
cycle
PlainFactorial.suspend
--> N := N + 1
F := F * N
V: var integer
V := PlainFactorial.getNext
V := PlainFactorial.getNext
==> V := PlainFactorial.getNext
V := PlainFactorial.getNext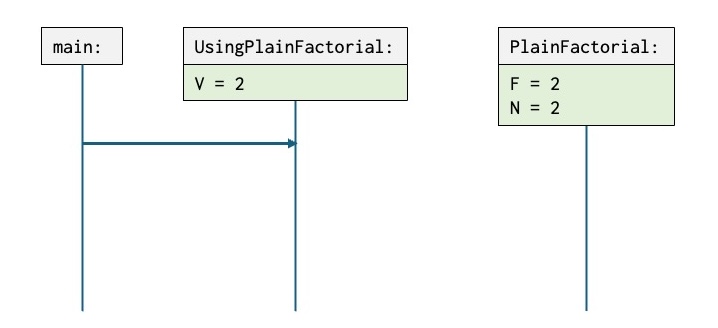
Finally we show a snapshot at the situation after execution of the last V := PlainFactorial.getNext:
PlainFactorialis (again) suspended before the statementN := N + 1.- The active point of execution is after the last statement.
- The variables
V,FandNhave been updated. V= 24 = 6!
UsingPlainFactorial: obj
PlainFactorial: obj
-"-
cycle
PlainFactorial.suspend
--> N := N + 1
F := F * N
V: var integer
V := PlainFactorial.getNext
V := PlainFactorial.getNext
V := PlainFactorial.getNext
V := PlainFactorial.getNext
==>
Burde måske stå noget om hvordan activities terminerer (rigtig ord?); det samme som ville sige når toppen på stakken terminerer.
Recursive factorial generator
Kommentarerne om main ovenfor gælder selvfølgelig også her, og hvordan man beskriver at at program udføres.
Next we show a a version of a factorial generator using a recursive method instead of the loop implemented using cycle. As said the purpose is to show how coroutines work and not necessarily a recommended programming style.
RecursiveFactorial: obj
getNext -> R: var integer:
RecursiveFactorial.call
R := F
F: var integer
N: var integer
next:
RecursiveFactorial.suspend
N := N + 1
F := F * N
next
F := 1
nextWhen RecursiveFactorial is generated it invokes the local method next, which suspends execution. Successive invocations of next resumes the coroutine and returns then next factorial (F) in the sequence.
The next figures shows snapshots of using RecursiveFactorial by the object UsingRecursiveFactorial:
UsingRecursiveFactorial: obj
RecursiveFactorial: obj
-"-
V: var integer
V := RecursiveFactorial.getNext -- V = 1
V := RecursiveFactorial.getNext -- V = 2
V := RecursiveFactorial.getNext -- V = 6
V := RecursiveFactorial.getNext -- V = 24 The first snapshot how the situation after the objects UsingRecursiveFactorial and RecursiveFactorial have been generated:
RecursiveFactorialis suspended beforeN := N + 1in the method objectnext.- Note that
RecursiveFactorialhas been suspended while execution an instance of the methodnext. - The active point of execution is at the first
V := RecursiveFactorial.getNextinUsingRecursiveFactorial. - The values of the variables are
V = 0,F = 1andN = 0.
UsingRecursiveFactorial: obj
RecursiveFactorial: obj
getNext -> R: var integer:
RecursiveFactorial.call
R := F
F: var integer
N: var integer
next:
RecursiveFactorial.suspend
--> N := N + 1
F := F * N
next
F := 1
next
V: var integer
==> V := RecursiveFactorial.getNext
V := RecursiveFactorial.getNext
V := RecursiveFactorial.getNext
V := RecursiveFactorial.getNext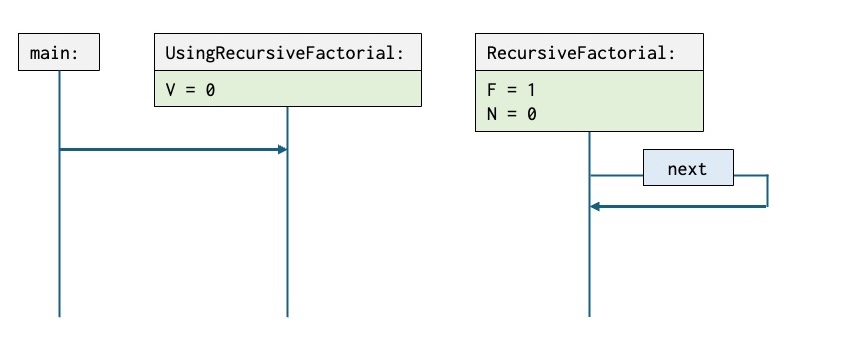
Her er det vel vigtig at få formidlet at RecursiveFactorial har en activity som bliver udført ved hver RecursiveFactorial.call.
The next snapshot shows a situation after execution of the first RecursiveFactorial.getNext:
RecursiveFactorialhas been resumed.N := N + 1has been executed —N = 1.F := F * Nhas been executed —F = 1.- A recursive invocation of
nexthas been generated. - The active point of execution is at
RecursiveFactorial.suspendin thisnextmethod.
UsingRecursiveFactorial: obj
RecursiveFactorial: obj
-"-
next:
==> RecursiveFactorial.suspend
N := N + 1
F := F * N
next
F := 1
next
V: var integer
V := RecursiveFactorial.getNext
V := RecursiveFactorial.getNext
V := RecursiveFactorial.getNext
V := RecursiveFactorial.getNext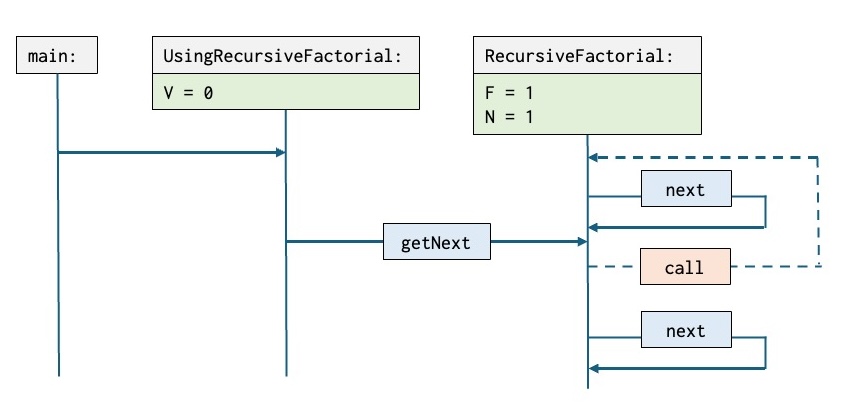
Har nu indsat en call i figuren med en speciel markering på pilen og farven
Det er ikke oplagt at metodekaldet med getNext skal pege som den nu gør på figuren.
Rækkefølgen af kaldene er fortsat korrekt.
Men stakken er stadig mudret.
Og der skal faktisk også en call ind på flere af de andre figurer hvis vi skal være konsistente!
call-pilen til et punkt før det første kald på kan nemt misforstås til at man da kalder den samme next igen, selvom jeg godt ved at pilen fra call ikke skal forstås sådan. Skal man først have denne notation for metodekald, så ville det næsten være bedre at call-pilen træffer lifeline under call.
Man skal vel kunne generere stakken ved at følge pilene, f.eks. …, getNext, next, next.
Synes dette bliver mere tydeligt med slide 14 i Coroutines-book.pptx! Også call-pilen.
OLM: lad os tage snakken ud fra denne – dem der pt er her skal laves om.

V := RecursiveFactorial.getNext -- V = 2V := RecursiveFactorial.getNext -- V = 6V := RecursiveFactorial.getNext -- V = 24
Plus more not shown
As can be seen, a suspend within next, suspends the whole execution stack and a call resumes execution of the top element of the stack. +++ Bedre formulering.
Merging binary search trees
The next example is more interesting. Here we show how to merge two binary search trees. We assume that the reader is familiar with the concept of a binary search tree +++ evt henvisning.
In this example, we define a binary tree where the a node contains a String being the name of a person. First we define class BinarySearchTree:
class BinaryTree:
class node(elm: var String):
left: ref node
right: ref node
insert(S: var String):
if (S <= elm) :then
if (left == none) :then
left := node(S)
:else
left.insert(S)
:else
if (right == none) :then
right := node(S)
:else
right.insert(S)
print(ind: var integer):
...
root: ref node
insert(S: var string):
if (root == none) :then
root := node(S)
:else
root.insert(S)
:::A BinaryTree has the following attributes:
- A local class
Node. - A reference
root, that refers to the root (topNode) of the tree. - A method
insertfor inserting aNodein the tree with the parameterSbeing theStringstored in theNode. It works as follows:- If
root == none, then the insertion is the firstNodeelseroot.insert(S)is invoked.
- If
- A
Nodehas the following attributes: - References
leftandrightthat refer to the left and right branches of theNoderespectively. - An
insertmethod that works as follows:- If
S <= elmwhereelmis the name in the currentNode, thenSis inserted in the left branch.- If
left == nonethenSis the first element in the left branch andleft := Node(S)is executed otherwiseleft.insert(S)is executed recursively.
- If
- If
S > elmthenSis inserted in the right branch.
- If
- A print
methodnot shown.
When a Node is inserted into the tree it is ordered based on a lexicographical ordering. I.e. “Dave” comes before “John” (“Dave” < “John”).
Preliminary figure
We may then declare two BinaryTree objects and insert some elements into them:
boys: obj BinaryTree
girls: obj BinaryTree
boys.insert("Peter")
girls.insert("Cecilie")
girls.insert("Maria")
boys.insert("Robin")
... Next we add a coroutine, theScanner, that traverse the tree and for each node in the tree, it suspends execution and returns the value at the node. If the tree has n nodes it returns a sequence of String values where V1 <= V2 <= V3 <= ... <= Vn.
class BinaryTree:
-"-
theScanner: obj +++ scanner
CV: var String
next -> V: var String:
theScanner.call
V := CV
scan(current: ref node):
if (current =/= none) :then
scan(current.left)
CV := current.elm
theScanner.suspend
scan(current.right)
theScanner.suspend
scan(root)
CV := ""
theScanner.suspend
next -> V: var String:
V := theScanner.nextFinally we may add a method, merge that merges the values of two binary search trees:
merge:
nextBoy: var String
nextGirl: var String
tail(T: ref BinaryTree):
cycle
S: var String
S := T.next
if (S = "") :then
leave(tail)
:else
S.print
nextBoy := boys.next
nextGirl := girls.next
loop: do
if (nextBoy <= nextGirl) :then
if (nextBoy = "") :then
nextGirl.print
tail(girls)
:else
nextBoy.print
nextBoy := boys.next
restart(loop)
:else
-- nextBoy > nextGirl
if (nextGirl = "") :then
nextBoy.print
tail(boys)
:else
nextGirl.print
if (nextBoy.length > 0) :then
nextGirl := girls.next
restart(loop)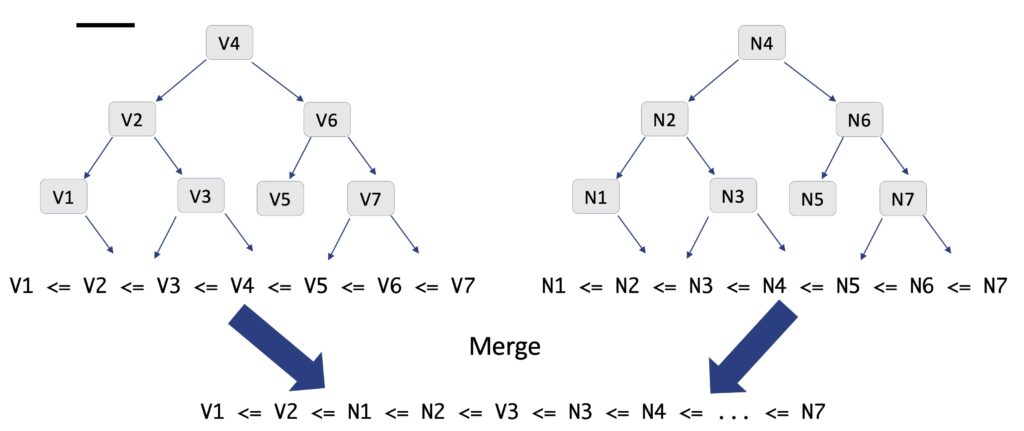
The merge method works ass follows:
- The statements:
nextBoy := boys.nextandnextGirl := girls.nextassigns the first boy and first girl tonextBoyandnextGirlrespectively where the ordering is alphabetical. - If
nextBoy <= nextGirl, thennextBoyis printed andnextBoyis assigned the next boy from the tree usingboys.next. - If
nextBoy > nextGirl, thennextGirlis printed and assigned the next girl. - This is repeated until no more boys and girls in the trees.
- The termination condition is that the empty string (
"") is returned bynextif no more girls/boys in a tree. - if the boys tree becomes empty before the girls tree, then the method invocation
tail(girls)prints the remaining girls in the tree – similarly if the girls tree becomes empty before the boys tree.
