10.1.3 An abstract syntax tree

In this section, we will show how to represent an expression by means of an abstract syntax tree. An abstract syntax tree (AST) or just syntax tree is a data structure that may represent the structure of a text described by a grammar.

The “tree” in AST refers to the fact that an AST is an example of a common data structure called a tree. A tree represents a hierarchical structure with a set of connected nodes. A node may have zero or more children which are also nodes. A child has exactly one parent. Nodes that have no children are called leaf nodes. The top node in a tree is called the root and have no parent.

A binary tree is a common used data structure where each parent has at most two children and the two nodes are often ordered in a left node and a right node.

For our expression grammar we will use a binary tree and the tree in the figure below shows a representation of the expression "10 + 11 * (1 + 9)".

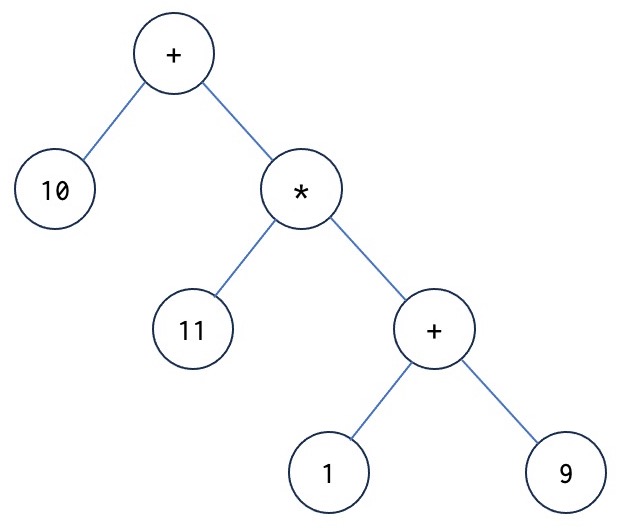
In the following, we introduce classes to represent a binary AST for our expression grammar as shown in the figure. We start by introducing a general class being the superclass of all nodes of an AST:

class Node(label: var char, left: ref Node, right: ref Node): 
   eval -> v: var integer:<
      inner(eval)
   print(ind: var integer):
         ...

Class Node has three parameters, the label of the node, and left and right representing the two children of the Node. In addition, a Node has an eval-method and a print-method. We return to these later in this section.

For each nonterminal except <Primary>, we have a subclass of Node:

class ExpNode: Node
   eval::
      v := left.eval + right.eval
class TermNode: Node
   eval::
      v := left.eval * right.eval
class NumberNode: Node
   eval::
      if (right == none) :then
         v := left.eval
      :else
         v := (left.eval * 10) + right.eval
class DigitNode: Node
   eval::
       v := label - '0'

The next figure shows how the above tree representing "10 + 11 * (1 + 9)" may be represented as objects of these classes:

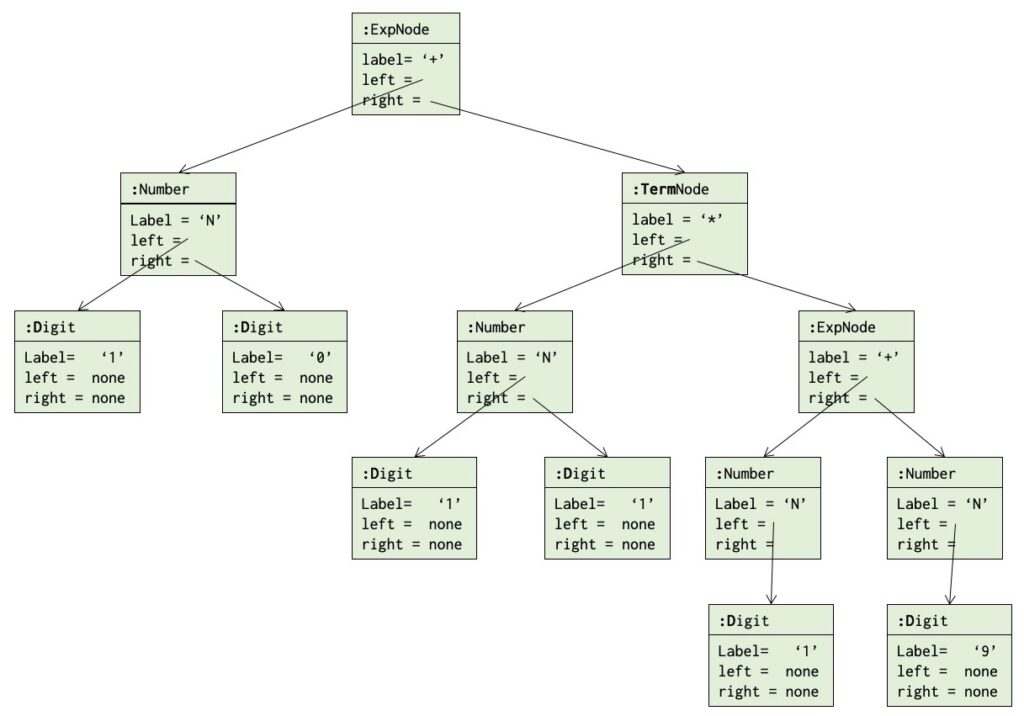
The eval-method performs a recursive traversal of the tree and evaluates the expression represented by the tree. If root is a reference to the root of the tree, root.eval will return the value 120.

Perhaps show a (sequence) diagram showing the traversal of eval in the AST?

Building the AST

We now extend the parser to build the AST during parsing. Each method will then return the AST for the string being parsed by the method. Consider exp:

exp -> N: ref Node:
   N := term
   addOp: do
      if (ch = '+') :then
         rN: ref Node
         nextChar
         rN := term
         N := expNode('+',N,rN)	
         restart(addOp)

As can be seen the return value of exp is a Node represented by the reference variable N. The method term is assumed to return the AST representing the string parsed by term.

If no '+' character is following the first call of term (ch = '+') then exp just returns the Node returned by term. If a '+' character is met, term invoked again, and exp returns an ExpNode with the first argument being a '+', and the second and third argument being the nodes returned by the first an second call of term. This is repeated as long as ch = '+'.

The revised methods term and primary may look as follows:

term ->  N: ref node:
   N := primary
   multOp: do
      if (ch = '*') :then
         rN: ref Node
         nextChar
         rN := primary	 
         N := termNode('*',N,rN)
         restart(multOP)
primary -> N: ref Node:
   if (ch = '(') :then
      nextChar        
      N := exp
      if (ch = ')') :then
         nextChar
      :else
         syntaxError(1)
   :else
      N := number

As can be seen, the structure of term similar to exp whereas primary just returns the Node returned by exp or number.

Next we show the revised versions of number and digit:

number -> N: ref node:
   N := digit
   moreDigits: do
      if (ascii.isDigit(ch)) :then
         rN: ref Node
         rN := digit
         N := NumberNode('N',N,rN)	    
         restart(moreDigits)
      :else
         N := NumberNode('N',N,none)
digit -> N: ref Node:
   if (ascii.isDigit(ch)) :then
      N:= digitNode(ch,none,none)
      nextChar
   :else
       syntaxError(2)

These should be straightforward to understand. Note, however, that both may return a Node where the left and/or right child is none.

Finally we may show the new version of the parse method:

parse:
   N: ref Node
   inn :=  "10 + 11 * (1 + 9)"
   console.print(("\nParse: " + inn + "\n")
   nextChar
   N := exp      
   if (ch <> ascii.null) :then
      syntaxError(3)
   if (not hasSyntaxErrors) :then
      console.print("\nResulting AST:\n")	  
      console.print(N.print(0))
      console.print("Evaluation of exp is: N.eval))

If no syntax errors have happened during the exp-call, the resulting AST is printed and the result of evaluating it is also printed.

We have not shown details of a print-method and leave this to the reader. The parameter of print is supposed to be the level of a given Node in an AST where the root is at level 0 and the children of the root at level 1, etc. This should make it easier to print an indented text version of the AST.